屋外広告士の知識

１．反力$H_A$、$V_A$、$V_B$を以下のように仮定する。

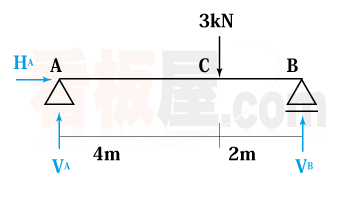
２．水平方向の力の釣合　$\Sigma{X}=0$ より
$H_A=0$

３．鉛直方向の力の釣合　$\Sigma{Y}=0$ より
$V_A-3+V_B=0$

４．$A$点まわりのモーメントの釣合　$\Sigma{M_A}=0$ より
$4\times3-V_B\times6=0$
$V_B=2kN$

５．４を３に代入すると
$V_A-3+2=0$
$V_A=1kN$

以上により、$H_A=0$、$V_B=2kN$、$V_A=1kN$となる。

１．反力$H_A$、$V_A$、$M_A$を以下のように仮定する。

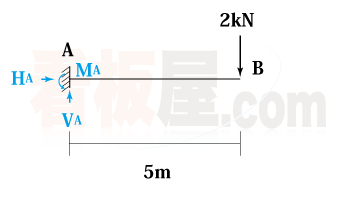
２．水平方向の力の釣合　$\Sigma{X}=0$ より
$H_A=0$

３．鉛直方向の力の釣合　$\Sigma{Y}=0$ より
$-2+V_A=0$
$V_A=2kN$

４．$A$点まわりのモーメントの釣合　$\Sigma{M_c}=0$ より
$M_A-2\times5=0$
$M_A=10kN$

以上により、$H_A=0$、$V_A=2kN$、$M_A=10kN$となる。

１．反力$R_A$、$R_B$を以下のように仮定する。

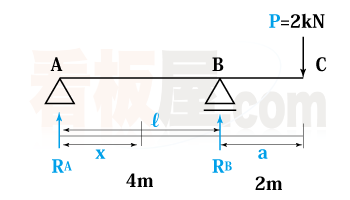
２．$R_A=-\frac{P\cdot{a}}{\mathit{l}}$ より

$R_A=-\frac{2\times2}{4}$

$R_A=-1kN$

３．$R_B=\frac{a+\mathit{l}}{\mathit{l}}P$ より

$R_B=\frac{2+4}{4}\times2$

※分数忘れている方のために丁寧に計算してみます。

$R_B=\frac{6}{4}\times2$

$R_B=\frac{12}{4}$

$R_B=3$

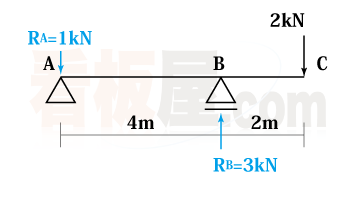
※$R_A$の値がマイナスだったということは、１で仮定した矢印の向きが逆だったという意味。